Physical Simulation-Bubble

1. Introduction

This is the report for reproduction of the paper, (Siggraph 2021)Thin-Film Smoothed Particle Hydrodynamics Fluid. This paper is about thin film in space, and topological deformation and thickness evolution on surface is simulated simultaneously.

2. Preliminaries

2.1 Lagrange Methods

• Q: What is Lagrange Methods?
• A: Fluid is discretized to particles and attributes of fluid are combined with particles.

Compared with Euler Methods…

• Merits：
  • Easy to parallism
  • Can simulate dramastic deformation
• Demerits:
  • Seeding and Reseeding need time
  • Not Suitable for incompressible fluid
    Dramastic deformation is widely spread in film simulation, like bubbles, so Lagrange Methods is taken.

2.2 SPH Methods

2.2.1 Formula

SPH (Smoothed Particle Hydrodynamics) is one of the popular Lagrange methods. It is inspired from the Dirac delta function：
$$
f(x)=\int_\Omega f(x’)\delta(x-x’)dx’, \delta(x-x’)=\begin{cases}\infty&x=x’\0&x\neq x’\end{cases}
$$
Delta function $\delta(x-x’)$ with a ‘point’ support and the equation for f(x) is not suitable to be discretized. Then a smoothing function $W(x-x’,h)$ is substitude it and $f(x)$ is approximated by
$$
<f(x)>=\int_\Omega f(x’)W(x-x’,h)dx’
$$

2.2.2 Kernel

The SPH method is $h^2$ accuracy and the kernel function W($\cdot$,h) must satisfy the following properties.

• Unity (make SPH accurate): $\int_\Omega W(x-x’,h)dx’=1$
• Cappcat support(can be computed by discretization): W(x-x’)=0, when $|x-x’|>kh$
• Pisitivity(satisfy physical scene): $W(x-x’)$
• Decay (nearer points influence more)
• Smoothness (can support differential on particals)
• Symmetric(even function)
• Delta function property(consider the nature)

2.2.3 Select Kernel

There are several kernels satisfying the property in 0.2.2, but people still select kernels cautiously. Different kenels have some slight differences but this small differences will lead to large difference in simulation.

This paper choose kerenels:
(1) Quartic spline Kernel (high order spline makes more closely approximation and more stable)
$$
W(R,h)=\begin{cases}
(R+2.5)^4-5(R+1.5)^4+10(R+0.5)^4&0\le R\le \frac{1}{48}h\
(2.5-R)^4-5(1.5-R)^4&\frac{1}{48}h\le R \le \frac{1}{16}h\
(2.5-R)^4& \frac{1}{16}h\le R\le \frac{5}{48}h\
0&R>\frac{5}{48}h
\end{cases}
$$

(2) Spiky Kernel(avoid clustering caused by inappropriate repulsive forces.)
$$
W_{spiky}(r) = \frac{15}{\pi h^{3}}(1 -\frac{r{3}}{h_{3}}) (0 \leq r \leq h)
$$

For more details, refer to Smoothed Particle Hydrodynamics (SPH): an Overview
and Recent Developments.

2.2.4 Differential on Particles

The main reason for the popularity of SPH in fluid simulation is that it support the differential on particles easily and the differential of the kernel function can be convert to the differential of the SPH kernel, which is easy and fixed. We will show the conversion for some differential operators below: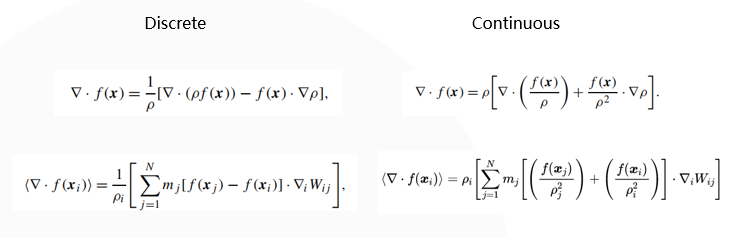

2.3 This Paper: SPH on Surface

• The original method does not take the pattern on the bubble and film seriously and only the topology deformation is considered. They implement the color pattern by adding some noise.