(2021-10-05)Games 102 Geometry-Review
由于课件内容较为清楚,此处仅总结重要内容以及其他内容的索引
1.通论
对应于课件1
- 计算机图形学:表现与表达三维数字对象

- 制作三维数据:几何数据,UV展开,纹理,材质,灯光,动画,…
- 几何内容的生成仍然是计算机图形学应用的瓶颈问题之一!
2. 函数拟合
对应于课件1,2 - 函数空间

空间的完备性:这个函数空间是否可以表示(逼近)任意函数? - 万能逼近定理(Weierstrass)
定理1:闭区间上的连续函数可用多项式级
数一致逼近
定理2:闭区间上周期为2π的连续函数可用
三角函数级数一致逼近 - 如何求满足要求的函数?

方法:
2.1 数据拟合
2.1.1 到哪找?
- 选择一个函数空间
RBF:径向基函数 https://www.cnblogs.com/hxsyl/p/5231389.html
成为核函数的基础:Mercer定理
https://baike.baidu.com/item/Mercer%E5%AE%9A%E7%90%86/19446322?fr=aladdin - 函数表达为基函数的线性组合
2.1.2 找哪个与怎么找?
2.1.2.1 目标1
- 函数要经过每一个数据点 插值(零误差)
- 联立,求解线性方程组(用插值多项式可以直接得到结果),但是它们的本质都和线性方程组相关
- 病态问题:系数矩阵条件数高时,求解不稳定.
- 插值函数的自由度=未知量个数-已知量个数
2.1.2.2 目标2
- 函数尽量靠近数据点(逼近)
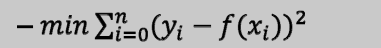
- 对个系数求导,得正规方程
2.1.2.3 避免过拟合的方法
- 基函数选择
- 岭回归(Ridge regression)–正则约束,还有方差正则项/系数正则项

- 稀疏正则化(冗余基函数,通过优化来选择合适的基函数)—把多余的基函数给筛掉
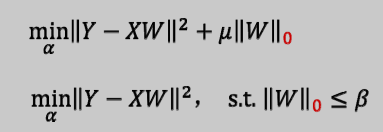 - 稀疏正则化从另一个角度理解:压缩感知(这里实际上是一个重建的问题)
- 稀疏正则化从另一个角度理解:压缩感知(这里实际上是一个重建的问题)
2.1.3 分段与光滑与逼近的比较
- 分段函数数据误差为0,但是只有C0连续,不光滑
- 光滑插值误差为0,但是可能被”差数据”带歪,导致函数性质不好,预测不可靠
- 逼近拟合函数虽然误差不为0,但是足够小
2.1.4 拟合方法
2.1.4.1 多项式插值
- 线性方程组矩阵为Vandermonde矩阵,方程组有唯一解
- 拉格朗日和牛顿计算公式
- 问题:系数矩阵稠密,依赖于基函数的选择,矩阵可能病态,导致难于求解(病态通过条件数衡量)

注:相关性的含义是说高次幂函数之间的差别越来越小,这样在拟合时,数据偏一点,就到另一条基函数上去了.
对于等距分布的数据点,范德蒙矩阵的条件数随着数据点数n呈指数级增长
好的基函数一般需要系数交替,互相抵消问题(防止基函数长得太近了)
解决方法L使用正交多项式基础
总结:多项式插值不稳定;Runge现象.
2.1.4.2 多项式逼近
为什么逼近?:数据点含噪声,更紧凑的表达,计算简单/更稳定
最小二乘逼近:
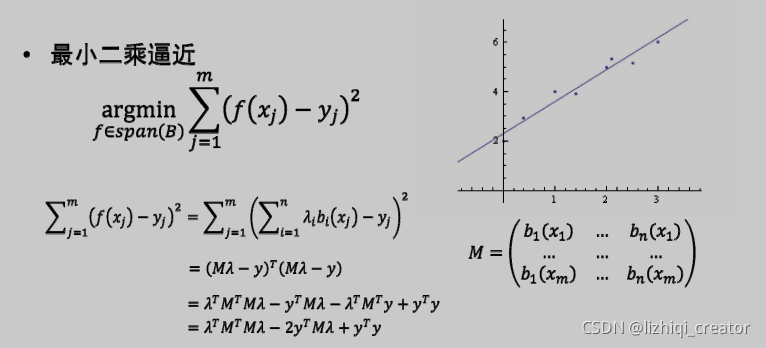

2.1.4.3 函数空间的选择
为什么使用多项式:稠密性与完备性—-表达能力足够
2.1.4.3.1 Bernstein多项式
可以使用Bernstein多项式做逼近

Bernstein多项式性质良好:凸包性,细分性,递归线性方程求解…
2.1.4.3.2 RBF函数插值/逼近
RBF函数
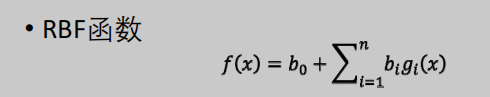
在一维空间中即为Gauss函数

现在的问题是RBF函数需要选择,太瘦了重叠部分太小,拟合程度不高
解决方法:将均值方差一起带进来优化(只要$a_i,b_i$足够多,也能够稠密)
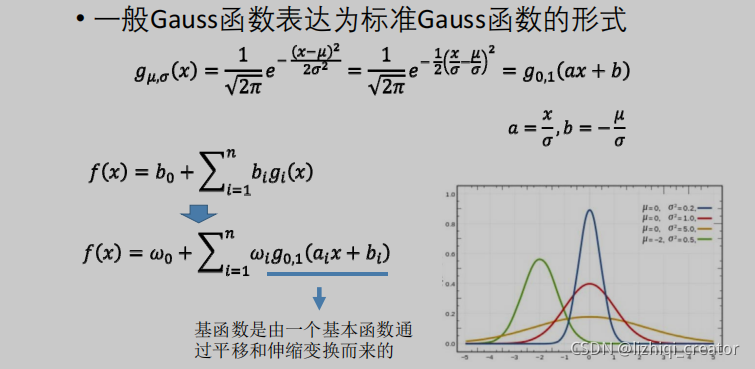
换个方式看:神经网络
2.1.4.3.2 神经网络优化
上面Guass函数拟合换个方式看:

神经网络的问题一般在于神经网络的结构与选择
Gauss函数的特性:拟局部性(不是凸的,只能得到局部值,比较适合神经网络来做).神经网络万能逼近定理

多层神经网络:多重复合的函数(一般来说,深的比宽的要好一些)
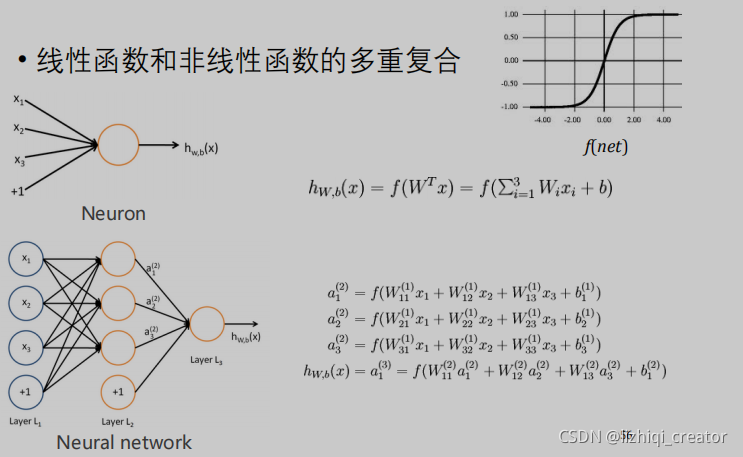
用神经网络来拟合函数

Why it works?
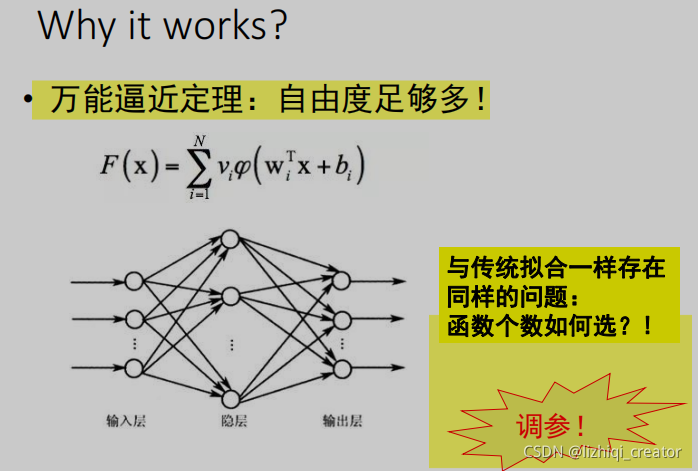
2. 曲线拟合
2.1 多元函数与映射
对应于课件3
2.1.1 多元函数
- 基函数构造:张量积

优点:定义简单;缺点:随着维数增加,基函数个数急剧增加,求解代价大 - 用神经网络表达

2.1.2 流形与映射
- 流形是一个从低维到高维的映射;任何一个点,无穷小区域等价于一个圆盘
- 降维映射(低维映射):降维映射一般有信息丢失,丢失的信息大部分不可逆,无法恢复.但是流形结构是可以恢复的.不可恢复优势也是有用的,比如提取信息,用于自编码器:m–>n–>m.
这也启示我们,调参的时候,隐藏层的维度不能太低,神经网络的本质:一个维度映射到另外一个维度 - 二维到二维的映射或者三维到三维的映射:plane warp/space warp
2.2 曲线拟合基础
对应于课件3
2.2.1 参数化问题
对应于课件3
观察上面误差度量的公式中,怎么知道数据点对应的参数?:这是个降维问题.求出参数后,然后极小化误差度量 - 参数化方法:


- 点的参数化对曲线拟合的影响很大
2.2.2 曲面参数化
对应于课件3
三维的点找二维的参数,降维问题
需要有好的几何性质,保局部的面积/长度/角度等几何性质,是好的.
- 应用:地图绘制,纹理映射
2.3 三次样条函数
对应于课件4

2.3.1 力学解释
见课件(贝努力-欧拉方程)
可以得到两压铁之间的函数为三次函数,即样条曲线为分段三次函数
2.3.2 数学性质
2.3.2.1 问题描述


2.3.2.2 解决方法

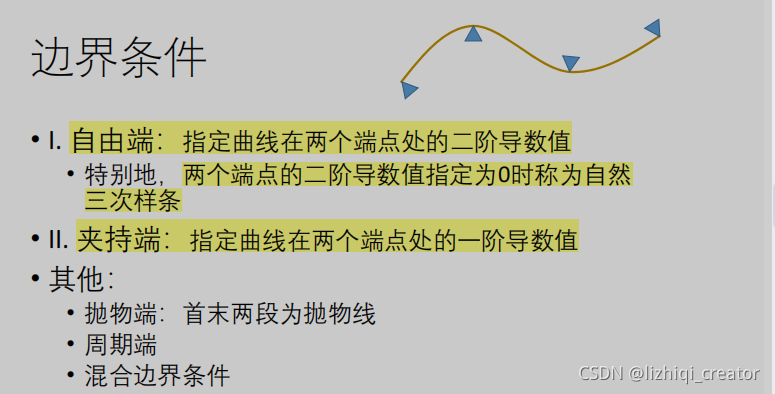


B样条教程:
https://blog.csdn.net/tuqu/article/details/5366701
2.3.4 三次样条的缺点

2.3.5 三次参数样条曲线

2.4 几何连续性
对应于课件4
- 参数连续性过于严格,在几何设计中不太直观.连续性依赖于参数的选择,同一条曲线,参数不同,连续阶也不同.只需要在某一段引入一个参数变化,就会导致不连续的产生.
- 几何连续性:

- 性质:

- 具体形式:

(G1实际上是将一个C1中的向量相等变成了方向相等)
2.4 Bezier曲线
对应于课件5
2.4.1 基本问题
(2021-10-05)Games 102 Geometry-Review
http://example.com/2023/01/10/2021-10-05-Games-102-Geometry-Review/